We assume a relationship of the form
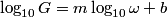 and attempt to calculate 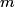 . Raising . Raising 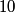 to the power of both sides, we see that to the power of both sides, we see that 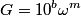 , so finding , so finding 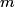 will allow us to distinguish between answers (B), (C), (D), and (E). From the two points will allow us to distinguish between answers (B), (C), (D), and (E). From the two points 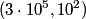 and and 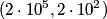 , we find that , we find that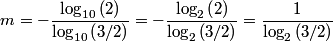 Since 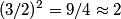 , , 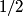 provides a better approximation to provides a better approximation to 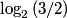 than than 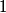 . Therefore, . Therefore, 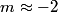 and answer (E) is correct. |